# Lecture 14 - AI Pathfinding ### SET09121 - Games Engineering <br /><br /> Kevin Chalmers and Sam Serrels School of Computing. Edinburgh Napier University --- # Recommended Reading - Artificial Intelligence for Games. Second Edition. Millington and Funge (2009). - Whole chapter on pathfinding.  --- ## Pathfinding 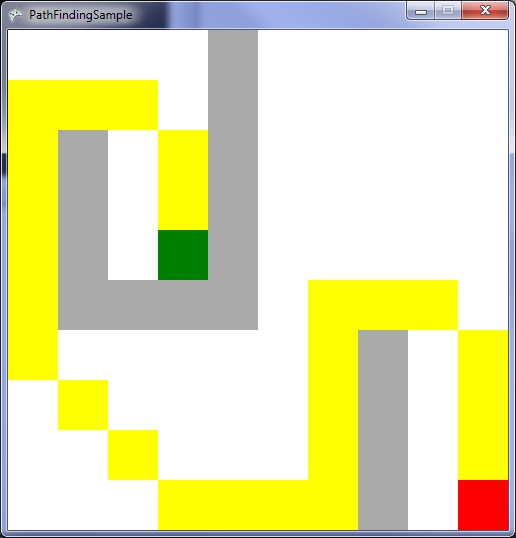 --- # What is Pathfinding? - Pathfinding (or more specifically path planning) is a decision making process that feeds into the movement. - You can consider it as crossing the boundary between movement and decision making. - Pathfinding is really the key ingredient to allow characters to navigate a map. - There is a good chance you have covered this before in AI or algorithms and data structures. --- # Why do we need Pathfinding? - Game maps are generally too complicated for simple steering to be in charge. - We could hard-code routes through the map, but that is not a scalable strategy. - So we need a technique that allows an entity to determine a route to follow to get to its destination. - Pathfinding allows us to do this -- it examines map data and provides a set of waypoints to follow by the entity. - Pathfinding is just a form of graph search, and there are different methods to do this. - We need a fast solution -- A* being the most commonly used. --- # Pathfinding Costs - Maps are very big today -- some over $100km^2$. - If each square metre was a navigation point that's $10^8$ points. - If we can travel in eight directions, things get very expensive. - Generally we are looking for simplifications to combat this. 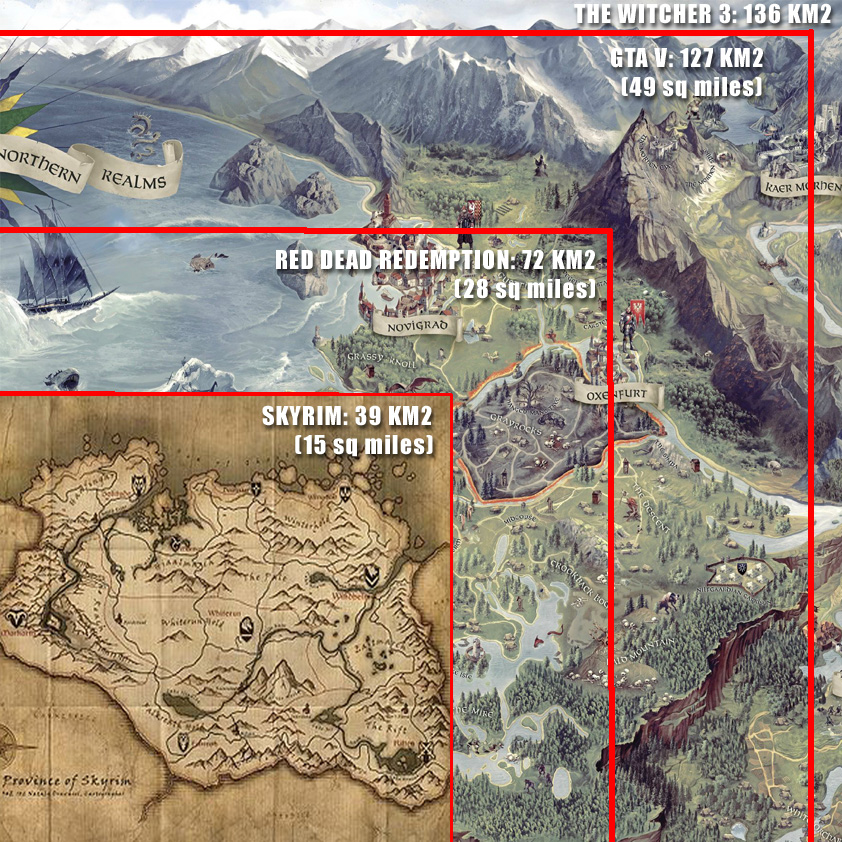 <!-- .element width="40%" --> --- ## Underpinning Theory -- Graphs --- # What is a Graph? - Prepare to have terms thrown at you which don't matter too much in this context. - A **graph** is just a collection of objects where pairs of objects are related in some way. - We typically refer to the objects as **nodes** (or vertices) and the connections as **edges**. - A graph can therefore be defined as a set of nodes and a set of edges. - From a game pathfinding point of view, a node is a location in the game world, and an edge is a path between two edges. - We don't need to be any more elaborate than that in game terms. --- # Example Graph -- Node-link Diagram  --- # Weighted Graphs - For pathfinding we are concerned with the cost. - The cost of a path is dependant on some factors (in games normally the distance) that allows us to determine what the cheapest path is. - We consider that an edge has a cost associated with it (weight) - To traverse an edge means to incur the cost of that traversal - In our pathfinding each traversal will have a cost of one 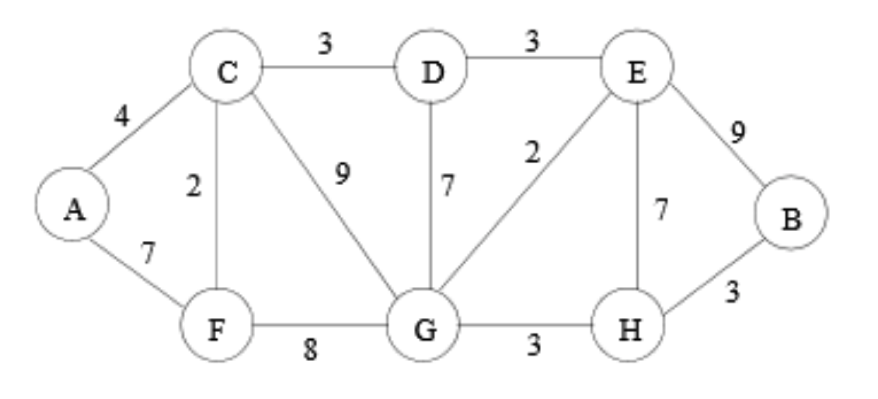 <!-- .element width="60%" --> --- # Directed Graphs - A graph may also be directed. - This means that an edge only has one direction of travel. - We won't use this, but it does exist in games. - For example, jumping down a ledge you cannot get back up.  <!-- .element width="60%" --> --- # Tile Engine and Graphs - We will be building our pathfinding into our tile engine. - It is just easier -- the data is all there. - We will use the data directly and build up our path incrementally from the level data. - The algorithm should be reusable though -- you just need to specify where you are getting the data from.  <!-- .element width="60%" --> --- # Tile Graphs - This approach should be OK for anything you are building, but a word of warning... - A tile-based graph pathfinding approach does not scale to large maps. - We mentioned this at the start. - A worst case pathfind means that all paths on all nodes have to be searched. - This leads to an algorithmic complexity of $\mathcal{O}(\lvert V \rvert^2)$. - $\lvert V \rvert$ is the size of the node (vertex) set. - So don't convert your massive million by million tile world into a pathfinding nightmare. --- ## Dijkstra --- # Dijkstra's Algorithm - Defined by Edsger Dijkstra in 1956. - An algorithm to find the shortest path between two nodes in a graph. - For a game, find the shortest path between two locations. - An extension to the algorithm allowed finding of all the paths from a source node. - In other words, how do we get to each of the nodes in the shortest time. - This algorithm is not only used for pathfinding in games. - Google Maps will use something similar for moving in road networks. - Network routing protocols will use such an algorithm. - Dijkstra is rarely used in games -- but the basic principles are. --- # Dijkstra's Algorithm - 6 steps 1. Mark all nodes as initially unvisited. Use this to create the set of *unvisited* nodes. 2. Set distances for the nodes: - Initial node (current node) distance is 0. - Other nodes set to infinity. 3. For the current node look at connected neighbours. Use to determine a tentative distance from the current node. Update the neighbours distances if the new route is shorter. 4. Mark current node as visited (remove from *unvisited* set). We will not visit this node again. 5. If destination has been marked visited (in other words we reached our destination) or all *unvisited* nodes have infinite distance, stop. 6. Else select unvisited node with smallest tentative distance from the initial node and set as current node. Go to step 3. --- # Dijkstra's Algorithm - Dijkstra is called a breadth-first search. - It iterates through nodes based on which one has the shortest distance from the start node. - This means it is not actively searching for the destination but doing a traversal of the graph until it happens to find it.  --- # Example -- Dijkstra at Work <iframe width="1400" height="800" src="https://www.youtube.com/embed/dhvf9KCAsVg" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen=""></iframe> --- # Problems with Dijkstra - The problem with Dijkstra's algorithm is it not actually searching for our destination. - Dijkstra's approach sets out to find the shortest path from a source to the neighbouring nodes. - It just might run into the destination at this step. - Therefore, Dijkstra is expensive for pathfinding - it might just get lucky. - This leads to an algorithmic complexity of $\mathcal{O}(\lvert V \rvert^2)$. - So we need a better technique that tries to find our destination node. --- ## A* --- # A* - A* was first described in 1968 (about 10 years after Dijkstra's algorithm) by a team from the Stanford Research Institute. - A* is called a best-first search or an informed-search algorithm. - This is because it takes into account a goal for working out which node to select next. - In a game our goal is the destination we want to get to quickest. - It does this by determining a cost for a node traversal based on whether it best meets the goal. - We can use different heuristics to evaluate these costs. - We will just use Euclidean (straight-line) distance. --- # A* also has 6 steps: 1. Mark all nodes as initially unvisited. Use this to create the set of *unvisited* nodes. 2. Set values for the nodes: - Initial node (current node) set to heuristic value. - Other nodes set to 0. 3. For the current node look at all the connected neighbours. Use this to determine a tentative cost (based on a heuristic). - Update the neighbours heuristic value if the new route is better. 4. Mark current node as visited (remove from *unvisited* set). We will not visit this node again. 5. If destination has been marked visited (in other words we reached our destination) or all *unvisited* nodes have infinite value, stop. 6. Else select unvisited node with best heuristic value and set as current node. Go to step 3. --- # A* - As stated, A* is a best-first search algorithm. - This means it doesn't select a shortest path from where it is, but chooses a node that looks like a better choice towards the goal. - However, in the worst-case A* still might have to search the entire graph. - We still have $\mathcal{O}(\lvert V \rvert^2)$ complexity.  <!-- .element width="40%" --> --- # Example -- A* at Work <iframe width="1400" height="800" src="https://www.youtube.com/embed/19h1g22hby8" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen=""></iframe> --- # Heuristics - There are different heuristics we can use to make the pathfinding act in a different manner. - The one we will use is Euclidean distance (straightline): $$h = destination - position $$ - Another is Manhattan distance: - $$ d = destination - position $$ - $$ h = \lvert d.x \rvert + \lvert d.y \rvert $$ - This might be more useful -- it is movement through a grid (either vertical or horizontal movement, no diagonal). Each movement costs 1 unit. - Chebyshev distance is similar to Manhattan but allows diagonal movement: - $$ d = destination - position $$ - $$ h = \max(\lvert d.x \rvert + \lvert d.y \rvert) $$ --- # A* versus Dijkstra <iframe width="1400" height="800" src="https://www.youtube.com/embed/g024lzsknDo" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen=""></iframe> --- ## Pathfinding and Steering --- # Output from Pathfinding - The output from a path finding or a path planning operation is called a *path* or *walk*. - There are different approaches we can take in a game: - A serious of directions of travel (useful for discrete movement). - A list of nodes to visit (better for continuous movement). - We will take the latter approach.  <!-- .element width="40%" --> --- # Pathfinding and Steering - Our aim is to use pathfinding as a decision making process for our movement. - The basic idea is that we have a starting position and a target position. - We use pathfinding to make a decision about how to move to the target position. - The list of nodes to visit then allows us to traverse the map using a steering behaviour. - The simplest approach is just to use an arrive behaviour for each node. Seeking will give you a wobble. - Combining steering behaviours, pathfinding, and physics will give you all the movement behaviour you need. --- ## Summary --- # Other Techniques - We have only looked at the main technique used in games but there are other considerations. - We talked about tactical path planning last week -- A* does let you consider this if your heuristic is done in that manner. - There are other tweaks to the pathfinding algorithms that can be done -- see the AI book. - There is also some work on pre-processing to better process the data. - Diffusion is another technique that works well for parallelisation on the GPU. --- # Summary - We've only covered the basics of pathfinding, but this is enough for what you need. - Pathfinding is really about finding the least expensive path to a destination. - This can obviously change based on the map changing. - Our use of pathfinding will get a list of nodes to visit and the subsequent use of this information to move a character around. - The lab will provide you with an algorithm that will work in the tile engine, but you should be able to extract the core idea if you need to.